Esté será un resumen de las métricas de regresión más comunes y en que situación usar cada una.
Métricas:
- Error cuadrático medio - MSE
- Raiz del Error cuadrático medio - RMSE
- Error absoluto medio _ MAE
- R al cuadrado, R cuadrado ajustado (R²)
MSE: Mean Squared Error
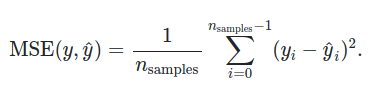
Es el promedio de la diferencia entre la predicción y el resultado real, al cuadrado.
Es una función de pérdida (loss function), así que siempre intentamos minimizarla.
Dado que está elevado al cuadrado, siempre va a ser positiva.
La medida de este error está al cuadrado de las unidades (si tenemos predicciones en centímetros, tendremos centímetros al cuadrado).
Una crítica que se le hace a esta métrica es muy sensible a los outliers, si todas las observaciones tienen el mismo peso.
La fórmula es semejante a la varianza.
RMSE: Root Mean Squared Error
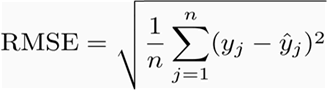
Es la misma fórmula que la métrica anterior, solo que es la raíz de la misma.
Esto nos permite tener la métrica en las mismas unidades que los datos, útil a la hora de representar la información.
La fórmula es semejante a la desviación éstandar.
No tenemos manera de saber la dirección del error.
Relacionando los posibles valores con lo anterior:
Si MSE es mayor a 1 => MSE <= RMSE:
mse = 5
rmse = sqrt(5)
>>> 2.23
Si MSE es menor a 1 => MSE > RMSE:
mse = 0.5
rmse = sqrt(0.5)
>>> 0.70
MAE: Mean Absolute Error
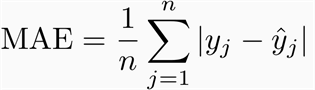
Es el valor absoluto del promedio de los errores.
No tenemos manera de saber la dirección del error.
Está en la misma unidad que la data que utilizamos.
No es derivable.
El error crece linealmente, 10 es peor que 1.
Es semejante a RMSE, pero tiene una diferencia importante (dado que la raíz está afuera cuando calculamos la media):
- para errores chicos se comportan más o menos igual.
- para errores grandes, RMSE le da más peso a los outliers (eso por el cuadrado, es más sensible a outliers). Es decir MAE es más robusto (menos sensible a outliers)
Ejemplo
from sklearn.metrics import mean_absolute_error as mae, mean_squared_error as mse
from toolz import partial
rmse = partial(mse, squared=False)
a = pd.Series([1,2,3,4,5])
b = a + 3
print(f'RMSE: {rmse(a,b)}', f'MAE: {mae(a,b)}')
>>> RMSE: 3.0 MAE: 3.0
b = a*10
print(f'RMSE: {rmse(a,b)}', f'MAE: {mae(a,b)}')
>>> RMSE: 29.8496231131986 MAE: 27.0
# para valores muy grandes se ve la penalización en el error.
b = a*100
print(f'RMSE: {rmse(a,b)}', f'MAE: {mae(a,b)}')
>>> RMSE: 328.34585424518457 MAE: 297.0
a = pd.Series([1,2,3,4,5])
b = a*100
b = b.append(a)
a = a.append(a)
# En este caso podemos ver que penaliza mucho los valores muy grandes
# Hay 5 muestras muy malas, y 5 muestras iguales.
print(f'RMSE: {rmse(a,b)}', f'MAE: {mae(a,b)}')
>>> RMSE: 232.17558011125976 MAE: 148.5
Entonces, ¿cuando deberíamos usar una sobre la otra? Depende el objetivo del problema.
- si queremos vender productos y queremos hacer una predicción de “cuantos”, decir +/- 10 utilizando MAE podría ser correcto, ya que tiene en cuenta el promedio de todos los errores.
- si queremos verificar la temperatura, y nuestro algoritmo debería ser más sensible a valores grandes (mucha temperatura en un instante puede ser un mal síntoma). En este caso preferiríamos usar RMSE.
R² __ Coeficiente de determinación
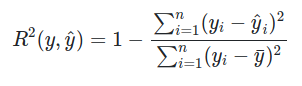
y_hat es la predicción y_i es el valor real luego está dividida por y_i - y_bar, donde y_bar es el promedio de todas las predicciones.
Lo que expresa es R² es la proporción de que tan bueno es nuestro modelo sobre un modelo más ingenuo (por y_bar)
R² es una medida que indica cuanta varianza de la variable dependiente es explicada por la variable independiente.
Puede tener valores negativos, indicando “muy malos resultados”.
No tiene unidades, lo que permite que sea más facil de interpretar entre distintos datasets y modelos.
Documentación Sklearn Investopedia Wikipedia
Keys & Refs
The most important metrics to evaluate a model are root mean squared error (RMSE) and R-squared (R²) - Practical Statistics for Data Scientists