Regression Metrics

3-minute read
machine-learning
metrics • machine-learning • regression

I’ve been writing a summary of the most common regression metrics, and when to use each one.

Metrics:

  • Mean Squared Error - MSE
  • Root Mean Squared Error - RMSE
  • Mean Absolute Error - MAE
  • R squared - R²

MSE: Mean Squared Error

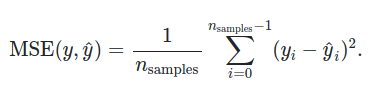
formula

It is the average between the differece of prediction and real data, squared. It is a loss function, so to optimize we will try to minimize it. Due to the squared part, it will be always positive. The measurement of the metrics is squared also. (cm -> cm²)
A criticism this metric receives is that it is very sensitive to outliers.

Sklearn Docs

RMSE: Root Mean Squared Error

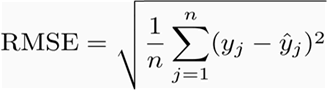
It is the same formula as above, however this is square rooted.

The measurement unit of this metric is the same as data due to square root(cm -> cm)

The error has not direction

Regarding to MSE and its values:

if MSE is greater that 1 => MSE <= RMSE:

mse = 5
rmse = sqrt(5)
>>> 2.23

if MSE is less that 1 => MSE > RMSE:

mse = 0.5
rmse = sqrt(0.5)
>>> 0.70

Link Wikipedia

MAE: Mean Absolute Error

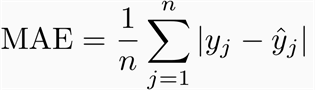
formula

It is the absolute error from the average prediction. The measurement unit of this metric is the same as data.
But this metric is not possible to derivate, due to absolute operator. The error is increase linearly, 10 is worse than 1.

Regarding to RMSE:

  • for small errors, it behaves similar.
  • for big errors, RMSE is more sensitive to outliers, so MAE is more robust.

i.e.:

from sklearn.metrics import mean_absolute_error as mae, mean_squared_error as mse
from toolz import partial

rmse = partial(mse, squared=False) 

a = pd.Series([1,2,3,4,5])
b = a + 3
print(f'RMSE: {rmse(a,b)}', f'MAE: {mae(a,b)}')
>>> RMSE: 3.0 MAE: 3.0

# for small errors, both behaves similar
b = a*10
print(f'RMSE: {rmse(a,b)}', f'MAE: {mae(a,b)}')
>>> RMSE: 29.8496231131986 MAE: 27.0

# for big errors, RMSE is more sensitive to outliers
b = a*100
print(f'RMSE: {rmse(a,b)}', f'MAE: {mae(a,b)}')
>>> RMSE: 328.34585424518457 MAE: 297.0

# 5 good samples, 5 bad samples.
a = pd.Series([1,2,3,4,5])
b = a*100
b = b.append(a)
a = a.append(a)

# In this case, RMSE increase more than MAE.
print(f'RMSE: {rmse(a,b)}', f'MAE: {mae(a,b)}')
>>> RMSE: 232.17558011125976 MAE: 148.5

So, which one should we use? It depends on the objective of our model:

  1. If we need to sell products, we are going to need “how much products”, and the errors could be… +/- 10. In this case, we could use MAE
  2. If we need to verify some temperature, the metric we should be sensitive to outliers, so we would rather select RMSE.

Link Wikipedia

R² - Coefficient of determination

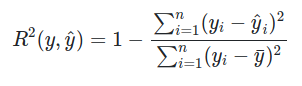
formula

y_hat is prediction
y_i is real value
Then divide by y_i - y_bar, where y_bar is the average from our predictions (the most common prediction).

R-Squared is a statistical measure of fit that indicates how much variation of a dependent variable is explained by the independent variable(s) in a regression model. Whereas correlation explains the strength of the relationship between an independent and dependent variable, R-squared explains to what extent the variance of one variable explains the variance of the second variable.

It could be negative, that indicates very bad results. It has not measurement unit, so it increases the interpretability between different models and datasets.

Documentación Sklearn Investopedia Wikipedia

Keys & Refs

The most important metrics to evaluate a model are root mean squared error (RMSE) and R-squared (R²) - Practical Statistics for Data Scientists

comments powered by Disqus